정수와 부동소수
컴퓨터가 숫자를 표현하거나 계산할 때 사용하는 두가지 방식
8 자리로 숫자표현을 할 때
- 12345678 과 같이 표현하면 표현의 범위는 1~99999999 까지이다.1)
- 1.2345678 과 같이 소수점 하나를 꼭 넣어서 표현하면 표현의 범위는 0.0000001 부터 9999999.9 까지이다.2)
위의 두가지 방식 중에 위의 것이 정수의 표현 방식이고 아래와 같은 방식이 부동소수(자리가 정해지지 않은 소수점)의 표현 방식이다.
따라서, 컴퓨터에서 제한된 자리수를 가지고 숫자를 표현할 때 부동소수 방식을 사용하면 훨씬 더 많은 범위 및 훨씬 해상도 높은 숫자(1.0000001~1.9999999 처럼 1 과 2사이를 엄청나게 세분화하여 표현 가능)를 표현할 수 있다. 다만 계산의 정확성은 정수형 표현이 정확하고 계산의 속도 또한 빠르다.3)
배정밀도
Double Precision
배정밀도(double precision)는 정수와 부동소수점을 모두 다루는 방법 중 하나입니다.
1. 정수형에서의 배정밀도: 정수형에서 배정밀도는 더 많은 비트를 사용하여 정수를 표현합니다. 예를 들어, 48비트 배정밀도 정수는 48개의 비트를 사용하여 정수를 나타내며, 부호 비트와 숫자 비트로 나뉩니다. 배정밀도 정수를 사용하면 더 큰 정수값을 표현할 수 있습니다. 이는 정수 데이터를 더 큰 범위로 표현하거나 더 높은 정밀도로 다룰 때 유용합니다.
2. 부동소수점에서의 배정밀도: 부동소수점에서 배정밀도는 더 많은 비트를 사용하여 부동소수점을 표현합니다. 일반적으로 배정밀도는 64비트를 사용하며, 부호 비트, 지수 부분, 그리고 가수 부분으로 나뉩니다. 배정밀도를 사용하면 더 큰 숫자를 더 정확하게 표현할 수 있습니다. 이는 과학 및 엔지니어링 분야에서 높은 정밀도의 계산이 필요한 경우에 유용합니다.
정수와 부동소수점에서의 배정밀도는 각각 데이터 형식에 따라 다르지만, 모두 더 큰 범위와 높은 정밀도를 제공하여 계산의 정확성을 향상시키는 데 사용됩니다.
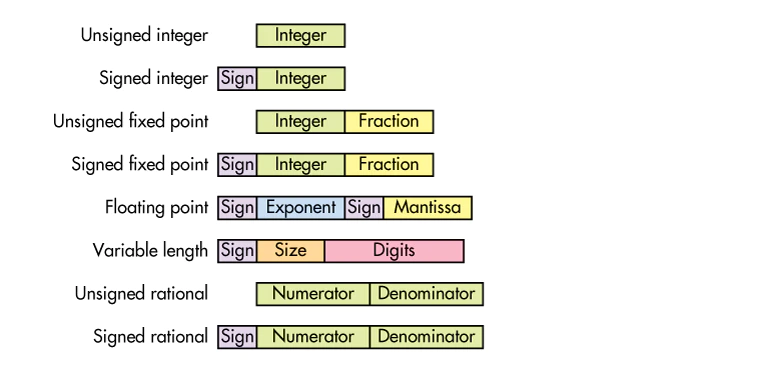
각 데이터 형식의 표현 범위
부동소수점 연산의 정밀성 손실
부동소수 연산의 정밀성 손실 문제를 구체적인 예시로 설명해보겠습니다.
예를 들어, 우리가 다음과 같은 두 개의 부동소수를 더한다고 가정해봅시다:
- 0.1 x 10-20
- 0.2 x 10-20
이 두 부동소수를 더하면 우리는 0.3 x 10-20이 나와야 한다고 예상할 수 있습니다. 그러나 컴퓨터에서는 부동소수점을 표현할 때 소수점 이하의 정밀도에 한계가 있기 때문에 정확한 결과를 얻기 어렵습니다.
실제로 컴퓨터에서 이러한 덧셈을 수행하면 다음과 같은 결과가 나올 수 있습니다:
- 0.1 x 10-20를 표현할 때 발생하는 정밀성 손실로 인해 실제로는 0.10000000000000000000005 x 10-20 정도로 저장될 수 있습니다.
- 0.2 x 10-20도 마찬가지로 정밀성 손실로 인해 0.20000000000000000000004 x 10-20 정도로 저장될 수 있습니다.
따라서 이 두 수를 더하면 0.30000000000000000000009 x 10-20 정도의 값이 나올 수 있습니다. 이것은 우리가 원했던 0.3 x 10-20과 약간 다른 값이며, 부동소수점 연산의 정밀성 손실로 인해 발생한 것입니다.4)
이러한 예시를 통해, 부동소수 연산에서의 정밀성 손실이 어떻게 발생하는지 좀 더 구체적으로 이해할 수 있습니다.
이러한 오차는 금융 분야에서의 시간, 금액 계산이나, 공학에서의 정밀 계산이 필요한 분야에서는 큰 오류를 범할 수 있지만, 그래픽 분야 또는 오디오 분야에서는 큰 문제가 되지 않습니다. 그래서, 그래픽 카드에서 쓰이는 GPU에서는 거의 부동소수형 연산자를 가진 칩을 사용하고, 오디오 쪽에서는 최근 부동소수형 DSP 칩들이 레이턴시가 짧아진 제품들이 나오면서5) 부동소수형 연산칩을 사용하는 경향이 있습니다.