목차

푸리에 변환

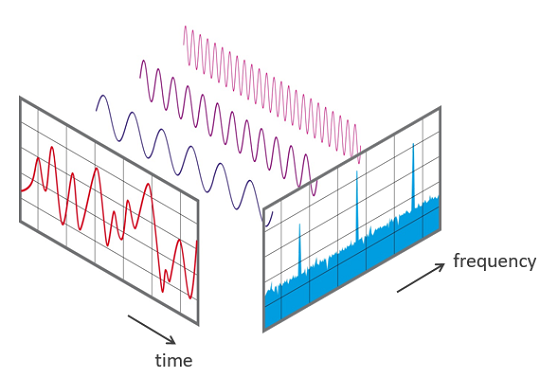
푸리에 변환(Fourier Transform)은 시간 영역에서 주파수 영역으로 신호를 변환하는 과정입니다. 이 변환이 주파수 영역에서 어떤 주파수 성분이 포함되어 있는지를 나타내며, 신호 분석, 필터링, 스펙트럼 분석, 신호 합성 등 다양한 응용 분야에서 중요한 역할을 합니다.

푸리에 변환의 주요 특징과 설명:

  1. 시간 영역에서 주파수 영역: 푸리에 변환은 시간 영역의 신호를 주파수 영역으로 변환합니다. 이것은 시간에 따른 신호의 주파수 구성을 확인할 수 있게 해줍니다.
  2. 주파수 성분 분석: 푸리에 변환을 통해 어떤 주파수 성분이 신호에 포함되어 있는지 알 수 있습니다. 이것은 음향 신호의 음원 분석, 스펙트럼 분석, 진동 해석 등에 사용됩니다.
  3. 역 푸리에 변환: 주파수 도메인에서의 정보를 시간 도메인으로 다시 변환하는 것을 역 푸리에 변환이라고 합니다. 이것은 주파수 도메인에서 필터링된 신호를 다시 시간 도메인으로 되돌리는 데 사용됩니다.
  4. 복잡한 신호 분석: 푸리에 변환은 신호를 간단한 주파수 성분으로 분해하는 데 사용됩니다. 이로써 신호 처리, 주파수 분석, 패턴 인식 등의 작업을 수행할 수 있습니다.

푸리에 변환은 다양한 분야에서 주파수 도메인으로 신호를 분석하고 처리하는 데 사용되며, 다양한 주파수 성분을 이해하고 조작할 수 있게 해줍니다.


Fourier Transform

Fourier Transform is a process that converts a signal from the time domain to the frequency domain. This transformation reveals which frequency components are present in the frequency domain and plays a crucial role in various applications such as signal analysis, filtering, spectrum analysis, and signal synthesis.

Key features and explanations of Fourier Transform:

  1. Time Domain to Frequency Domain: Fourier Transform converts a signal from the time domain to the frequency domain. This allows us to examine the frequency components of a signal over time.
  2. Frequency Component Analysis: Fourier Transform enables us to determine the frequency components present in a signal. This is particularly useful for tasks like analyzing audio sources, performing spectrum analysis, and vibration analysis.
  3. Inverse Fourier Transform: The process of reversing the transformation from the frequency domain to the time domain is known as the Inverse Fourier Transform. It is used to convert filtered signals from the frequency domain back to the time domain.
  4. Analysis of Complex Signals: Fourier Transform is used to break down complex signals into simpler frequency components. This facilitates tasks such as signal processing, frequency analysis, pattern recognition, and more.

Fourier Transform is widely employed across various fields to analyze and manipulate signals in the frequency domain, allowing us to understand and manipulate different frequency components.

FFT

Fast Fourier Transform, 고속 푸리에 변환

https://ko.wikipedia.org/wiki/%EA%B3%A0%EC%86%8D_%ED%91%B8%EB%A6%AC%EC%97%90_%EB%B3%80%ED%99%98