피타고라스 음률
Pythagorean temperament
한 음을 울렸을 때 등장하게 되는 기음과 배음의 구조 속에서 음계를 분리해 내어서, 음악적으로 멜로디를 짓는데에 사용하는 음계로 사용하기 위해서, 피타고라스는 3:2 의 간격을 이용해서 모든 배음들을 찾아내려고 하였다.
사실 지금 생각해보면, 계측 장치도 좋고, 주파수를 찾아내는 기계도 있기 때문에, 뭐하러, 3:2 의 간격을 이용해서 음계를 만드는데 썼을까? 하고 의문이겠지만, 피타고라스가 있던 시기에는 정확하게 그 음계를 찾아낼 방법이 3:2 의 간격을 이용하는 방법 외에는 없었기 때문이다.
어쨋든 음계를 구성하는 배음을 찾아내는 법칙은 다음과 같다.
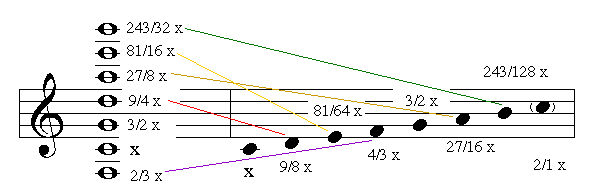
- 가장 기본적인 옥타브 음은 2:1 로 정한다
- 완전 5도인 간격을 이용해서 완전 5도음을 3:2 로 정한다.
완전 5도는 옥타브와 완전 4도의 간격을 이룬다. 계산을 이용해 완전 4도를 구한다.(완전 5도의 완전4도는 옥타브 ⇒ 완전5도 * X = 옥타브 )
3/2 * X = 2 , X = 2 * 2/3
2/3 *2 = 4/3장 2도인 간격은,앞서서 구해진 완전 4도와 완전 5도의 간격이 장 2도 이므로, 그 값을 구해 낸다 (완전4도의 장2도 는 완전 5도 ⇒ 완전4도 * X = 완전5도)
4/3 * X = 3/2 , X= 3/2 *3/4
3/2 * 3/4 = 9/8장 3도인 간격은, 장 2도의 장2도를 구해서 구해 낸다.
9/8 * 9/8 = 81/64장 6도인 간격은, 완전5도의 장 2도를 구해낸다.
3/2 * 9/8 = 27/16장 7도인 간격은, 장6도의 장 2도를 구해낸다.
27/16 * 9/8 = 243/128
이렇게 하여 구해진 음계는 계산상으로는 완벽해 보인다.
하지만 실제로 사용해보면 맞지 않는다.
왜냐하면 3:2 를 이용한 완전 5도의 음정과 4:3 을 이용해서 구해내는 완전 4도의 음정으로, 계속 계산을 하다보면, 같은 음이 나와야 하는데, D#=Eb
- 완전 5도씩 : A –> E –> B –> F# –> C# –> G# –> D#
- 완전 4도씩 : A –> D –> G –> C –> F –> Bb –> Eb
그 계산 값이 각각, 256:243 과 2187:2048로 다르다는 데에 문제가 있다. 단순히 완전 5도 만을 이용해서 스케일을 찾아내는 데에 문제가 있었던 것이다.
그래서 단선율을 연주하기에는 괜찮게 들리지만, 3화음을 연주 할 수 없었다.
| 음 | C4 | D4 | E4 | F4 | G4 | A4 | B4 | C5 |
|---|---|---|---|---|---|---|---|---|
| 비율 | 1:1 | 9:8 | 81:64 | 4:3 | 3:2 | 27:16 | 243:128 | 2:1 |
| cent | 0 | 204 | 408 | 498 | 702 | 906 | 1110 | 1200 |
| 차이 | 204 | 204 | 90 | 204 | 204 | 204 | 90 |