배음
배음(Harmonics)은 기음(Fundamental)의 주파수를 기준으로 생성되는 정수배 주파수의 성분들을 의미합니다. 기음은 음악이나 소리에서 가장 낮은 주파수 성분으로서, 이 기음 주파수에 정수배를 곱하여 만들어지는 주파수들이 배음입니다.
간단하게 말하면, 배음은 기본 주파수의 배수로 나타나는 주파수 성분들로, 원음의 특성을 반영하는 주파수 성분들을 말합니다. 배음은 원음의 특정 특성과 음색을 결정하는 데에 큰 영향을 미치며, 악기나 음성의 특징적인 소리를 형성하는 요소 중 하나입니다.
예를 들어, 어떤 악기에서 C4 (도4) 음의 기음 주파수가 261.63Hz라고 가정합시다. 그렇다면 배음은 이 기음 주파수의 정수배로 이루어질 수 있습니다. 2배음은 2 x 261.63Hz = 523.25Hz이며, 3배음은 3 x 261.63Hz = 784.88Hz입니다. 이런식으로 계속해서 배음이 형성됩니다.
기음과 배음들이 함께 합쳐져서 복합음(Complex tone)을 만들게 되며, 이 복합음이 악기의 음색을 결정하고 음악적 특성을 형성합니다. 배음들은 원음과 어떻게 상호작용하느냐에 따라 악기의 특징을 부각시키거나 다양한 음색과 효과를 만들어냅니다.
또한, 배음들은 음악의 조화와 화성에서도 중요한 역할을 합니다. 화성은 여러 음의 조합으로 이루어진 코드로, 배음들의 조합은 화성의 다양한 형태를 만들어냅니다. 음악 이론에서 배음들은 화성의 흐름을 이해하고 설명하는 데에 필수적인 개념 중 하나입니다.
Harmonics
Harmonics refer to the components in music or sound that are integer multiples of the fundamental frequency, which is the lowest frequency component known as the “fundamental.” In simpler terms, harmonics are frequency components that appear as multiples of the fundamental frequency, reflecting the characteristics of the original sound. Harmonics play a significant role in shaping the timbre and unique qualities of a musical instrument or voice. They are essential elements in defining the sound color and are a fundamental factor in forming the distinctive sound of instruments or voices.
For example, if we assume the fundamental frequency of a C4 note to be 261.63Hz for a particular instrument, the harmonics can be generated as integer multiples of this fundamental frequency. The second harmonic would be 2 x 261.63Hz = 523.25Hz, and the third harmonic would be 3 x 261.63Hz = 784.88Hz, and so on. This process continues to create harmonics.
When the fundamental and its harmonics combine, they form a complex tone, which determines the timbre of the instrument and contributes to its musical characteristics. The interaction between the harmonics and the fundamental can emphasize specific instrument characteristics or create various tonal colors and effects.
Furthermore, harmonics play a vital role in music harmony and chord progressions. Harmony, which consists of combinations of multiple notes, is influenced by the combinations of harmonics and is essential for understanding and explaining the flow of harmony in music theory. Harmonics are one of the fundamental concepts for comprehending the structure and character of musical sounds.
파형
Waveform
이 세상의 모든 존재하는 소리는 수 많은 배음들로 이루어져 있다. 그 중에는 그 소리의 음정을 알게 해주는 가장 낮은 배음인 기음이 있고, 그 기음에 색체감을 더해주는 배음들이 있다.이러한 기음과 배음은 모두 순수한 진동인 사인파이다.
따라서, 이것을 알기 쉽게 다르게 이야기해보면 “이 세상에 존재하는 모든 파형은 여러개의 사인파가 합쳐져서 이루어진 것”이라고 할 수 있다.
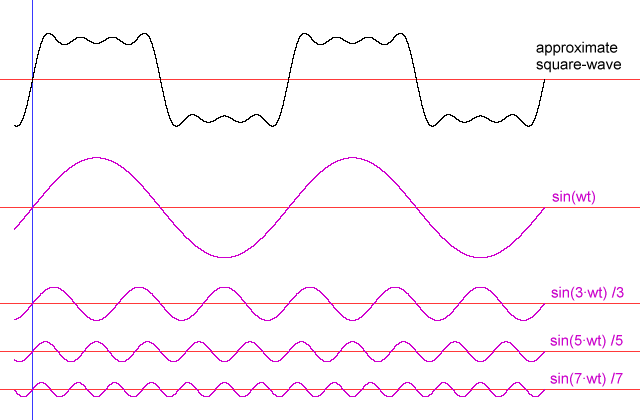
아래 그림은 몇가지의 사인파를 합하여서 사각파를 만들어 내는 것을 설명한다.
우선 기음에 1/3 크기의 3배음을 빼고, 다시 1/5크기의 5배음을 더하고, 1/7 크기의 7배음을 빼면, (빼는 것은 진동의 주기 시작을 변환하면 더하는 과정으로도 볼 수 있다.) 미약하게나마 사각파에 근접한 파형을 얻어내었다. 이러한 과정을 계속해서 반복하면, 사각파에 대한 오차를 계속 줄여나갈 수 있다. 언젠가는 완벽한 사각파의 모양을 만들어 낼 수 있다.
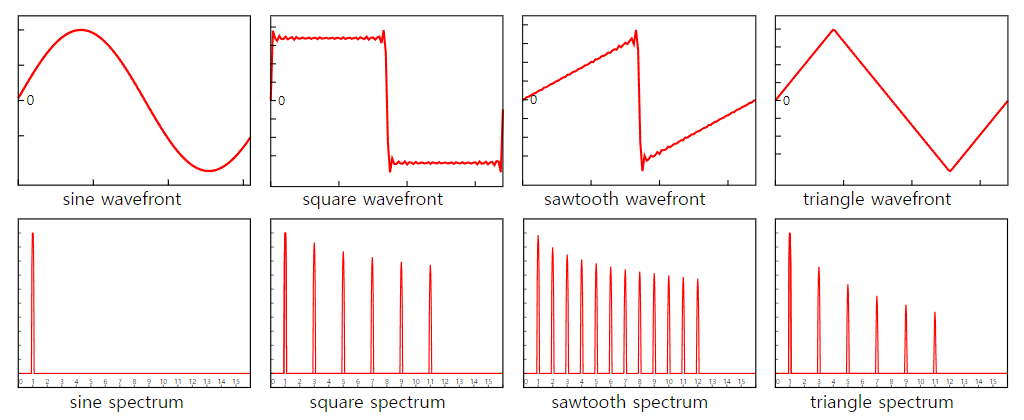
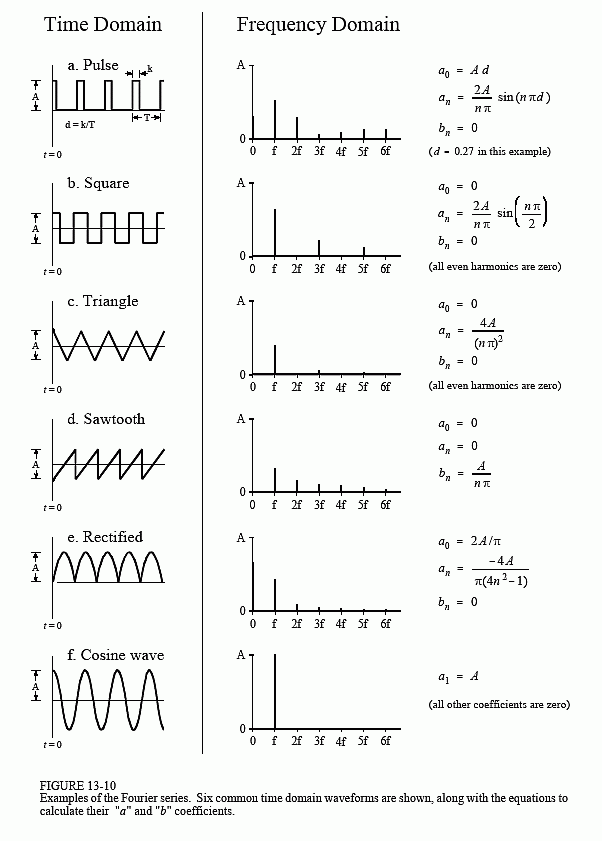
이러한 사인파들로 이루어진 기음과 배음을 조합하여 단순한 파형들을 만들어내는 공식들이다. 왼쪽에는 파형의 모습을, 오른쪽엔 배음구성과 공식을 보여준다.
물론 자연계에 존재하는 악기들의 파형이나 배음 구조는 이것들보다 훨씬 복잡하지만, 삼각파, 정현파, 톱니파, 사각파 등은 모두 음색이 다르고, 음색 합성의 기본 단위들로 많이 쓰인다.
배음이 가장많은 파형은 톱니파이고, 대체적으로 짝수차의 배음이 많이 포함되면 파형이 기울어지는 것을 알 수 있다. 2f, 4f 등의 짝수배수의 배음들은 대체적으로 기음에 대해 옥타브 관계이거나, 5도 화성이고, 3f, 5f 등의 홀수배 배음들은 대체적으로 3도, 7도 등의 화성인것과도 연관이 있을 것이다. 예를 들자면, 오디오에서 말하는, 진공관 방식의 증폭과, 트랜지스터 방식의 증폭에 있어서도, 짝수 배음이 생성되느냐, 홀수 배음이 생성되느냐의 문제를 이야기 하면서, 음색을 비교하기도 한다(프리앰프는 음색을 증폭하면서 배음을 생성한다. 왜곡이 있다는 이야기와도 같다.)
이러한 프리앰프의 증폭에서도 배음이 옥타브나 완전5도 화성이 등장하는가, 3도나 7도 화성이 등장하느냐에 따라서도 음색의 특성이 나타난다고 볼 수 있다.
따라서, 음색 합성에있어서, 대부분의 감산 합성 방식의 아날로그 신디사이저들은, 홀수배의 배음이 가장 많은 파형인 사각파와, 짝수배의 배음이 가장 많은 톱니파를 가지고, 음색 합성을 시작한다. 만약 사각파만 가지고 시작한다면, 짝수배의 배음을 절대 얻지 못할 것이고, 톱니파만 가지고 시작한다면, 홀수 배음만 가진 파형을 얻지 못하기 때문에, 보통 두가지로 시작한다.
파형을 가산하여서 음색을 합성하려면, 배음의 수 만큼의 VCO가 필요하지만, 감산 합성을 하면, VCO로 이미 배음이 많은 주어진 2개의 파형을 만들고, 여러가지 필터를 통해서 배음을 감산해버리면, 원하는 음색을 만들기 쉽기 때문이다.
사인파
Sine wave
푸리에 이론에서는 사인파를 “순수”한 파형으로 정의합니다. 푸리에 이론에 의하면 자연계에 존재하는 모든 가능한 파형은 사인파의 합으로 이루어져 있습니다. 사인파에는 기음 성분만 있고 배음 성분이 없습니다. 따라서 사인파에 필터를 적용해도 소리크기가 변할수는 있어도 아무런 효과가 없습니다. 이러한 이유로 사인파는 감산합성 방식에는 그다지 유용하지 않습니다. 감산합성 방식에서 일반적으로 사용되는 기본 파형은 삼각파, 펄스파, 톱니파입니다.
사각파
Square wave
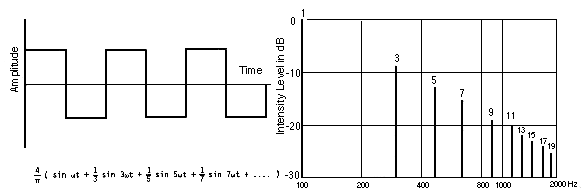
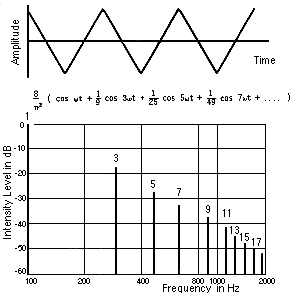
수평 중앙선을 기준으로 번갈아가며 직사각형으로 나타나는 파형입니다. 정사각파로 인정되려면 수평 중앙선 위와 아래의 직사각형이 동일한 폭이어야 합니다. 정사각파의 배음 분석 결과, 삼각파와 마찬가지로 짝수 배음이 없으며, 그러나 홀수 배음(특히 3번째, 5번째 및 7번째)이 삼각파보다 훨씬 두드러집니다. 원시적인 정사각파의 소리는 코를 막은 채로 노래하는 것과 유사한 비음질적인 특성을 가지고 있습니다.
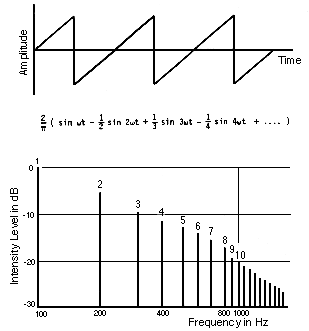
사각파는 기음 + 1/3 3배음 + 1/5 5배음 +1/7 7배음..계속.. 으로 굉장히 큰 홀수 배음들로 구성되어 있다.
펄스파
Pulse wave
번갈아가며 수평 중앙선 위와 아래의 직사각형으로 나타나는 파형입니다. 수평 중앙선 위와 아래의 상대적인 폭은 파형의 배음 성분에 영향을 미치는데, 특히 파형에 포함된 짝수 배음의 양에 관련이 있습니다. 상대적인 폭은 주로 파형이 수평 중앙선 위에 있는 시간의 백분율로 표현되며, 이것을 듀티 사이클 또는 펄스폭 비율이라고 합니다. 예를 들어, 75%의 펄스폭 비율은 파형이 수평 중앙선 위에 있을 시간의 3/4이고 수평 중앙선 아래에 있을 시간의 1/4임을 의미합니다. 10%의 펄스폭 비율은 수평 중앙선 위의 매우 좁은 부분이고 나머지 시간은 수평 중앙선 아래에 있습니다. 상단 및 하단 부분이 같은 폭인 50%의 펄스폭 비율은 보통 정사각파로 불립니다. 펄스폭 비율이 50%에서 멀어질수록(어느 쪽으로든) 짝수 배음 성분의 비율이 증가합니다.
톱니파
Sawtooth wave
이 파형의 배음 성분은 일반적인 VCO에서 생성되는 다른 파형과는 달리 상당한 양의 짝수 배음을 포함하고 있습니다. 청취 결과는 색소폰이나 목관악기와 약간 비슷한 소리입니다.
톱니파는 단순 파형들 중에서 가장 배음을 많이 가진 파형으로 배음 공식이
기음+ 1/2 2배음 + 1/3 3배음 + 1/4 4배음 + 1/5 5배음..계속..으로 사각파형이 홀수 배음만 지닌 것에 비해 짝수차수의 배음들 또한 가지고 있어 배음이 가장 많은 파형이다.