음향:signal_processor:filter:filter_topology
[홈레코딩 필독서]"모두의 홈레코딩"구매링크
가성비 있는 녹음실 찾으시나요? 리버사이드 재즈 스튜디오에서 녹음하세요!
[공지]회원 가입 방법
[공지]글 작성 및 수정 방법
목차
필터 토폴로지
Filter Topology
필터 토폴로지는 전자 회로 설계에서 필터를 구성하는 방법을 의미하는 용어입니다. 필터는 특정 주파수 대역을 통과시키거나 차단하기 위해 사용되며, 다양한 회로 구성 방식에 따라 성능과 특성이 달라집니다.
필터 토폴로지에는 여러 가지 종류가 있으며, 각 토폴로지는 주파수 응답, 위상 특성, 회로 복잡도에 영향을 미칩니다.
Bessel
Butterworth
- 이름의 유래 : 유명한 영국 물리학자 스티븐 버터워스(Stephen Butterworth)에서 이름을 따옴.
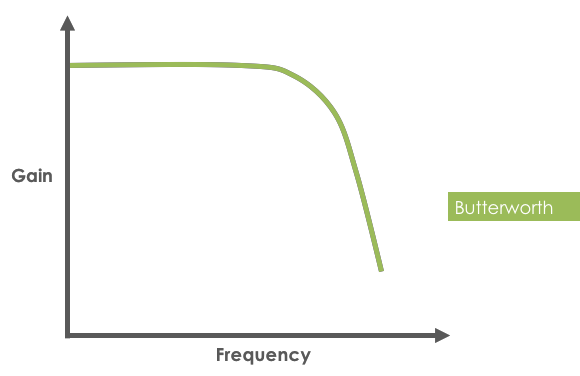
- Butterworth 필터 응답 :
Chebyshev
- 이름의 유래 : 러시아 수학자 파프누티 체비쇼프(Pafnuty Chebyshev)에서 이름을 따옴.
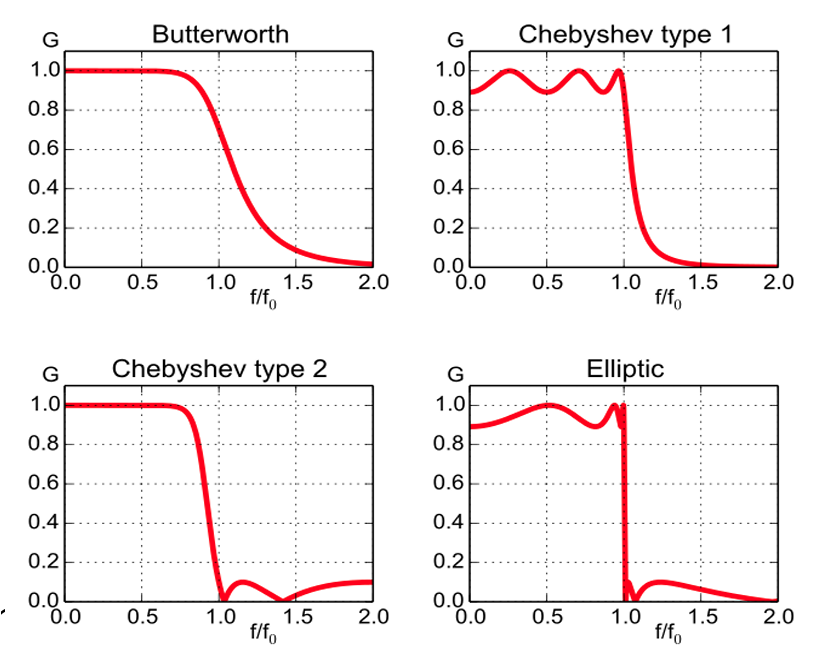
- Chebyshev 필터 응답 :
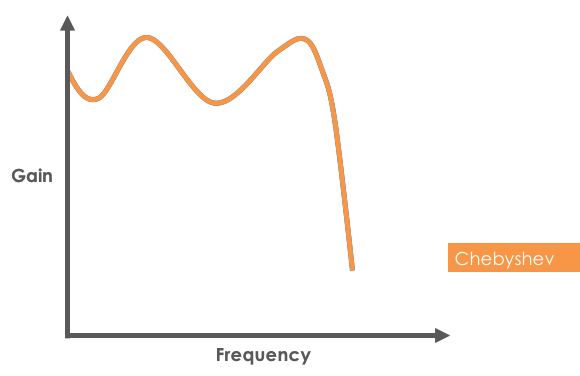
- 주요 특징 : Chebyshev 필터는 리플 응답으로 잘 알려져 있습니다. 이 리플 응답은 통과 대역(Chebyshev 1형) 또는 차단 대역(Chebyshev 2형)에서 나타나도록 설계할 수 있습니다. 리플의 크기는 롤오프(감쇠)의 가파름에 비례합니다. 즉, 더 가파른 응답을 원할 경우 리플 응답이 커집니다. 이러한 필터는 Elliptic 함수 필터와 Butterworth 필터의 중간 성능을 제공합니다. Chebyshev 필터의 위상 응답은 비교적 비선형적이며, 이는 결국 변조 해독기에 혼란을 초래합니다. 이는 비선형 지연으로 인해 펄스가 왜곡되기 때문입니다. 이 문제에 대한 가장 일반적인 해결 방법은 Chebyshev 필터의 대역폭을 늘려 이 비선형 영역을 더 먼 곳으로 밀어내는 것입니다.
Elliptic(Cauer)
- 이름의 유래 : 독일 수학자 빌헬름 카우어(Wilhelm Cauer)에서 이름을 따옴.
- Elliptic 필터 응답 :
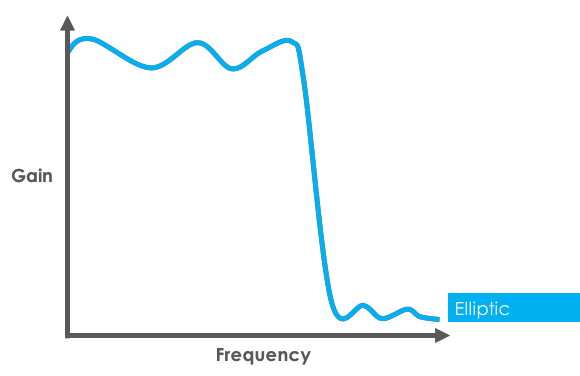
Linkwitz-Riley
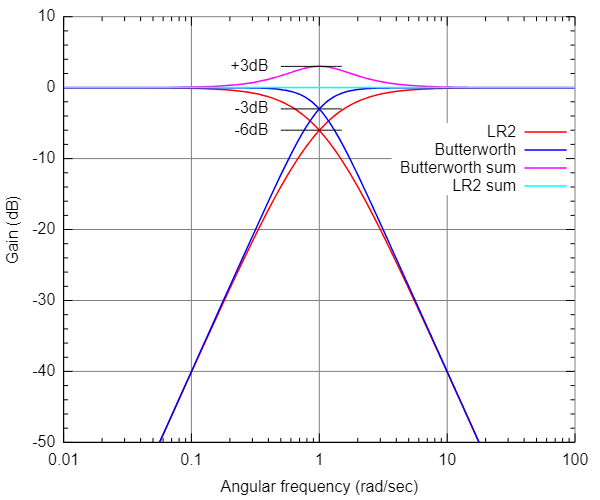
Linkwitz-Riley 필터는 저역 통과 필터와 고역 통과 필터를 병렬로 결합하여 크로스오버 주파수에서 이득이 0이 되도록 설계되었습니다. 크로스오버 주파수에서 이득이 0이므로, Linkwitz-Riley 필터는 전파 필터처럼 동작하여 평탄한 진폭 응답과 부드럽게 변화하는 위상 응답을 제공합니다.
Linkwitz-Riley 필터는 두 개의 Butterworth 필터를 결합하여 만듭니다.
두 필터의 주요 차이점은 Butterworth 크로스오버는 필터 차단 주파수에서 3dB 감소하는 반면, Linkwitz-Riley 필터는 평탄하다는 것입니다.
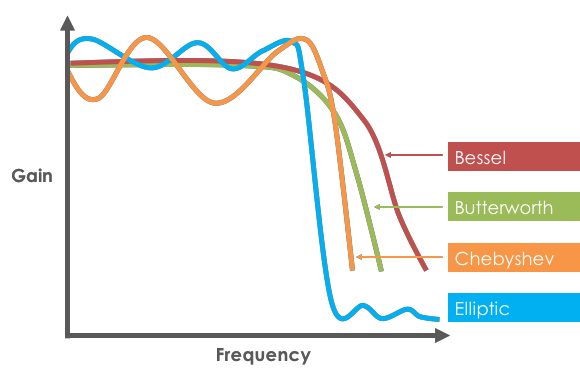
Bessel, Butterworth, Chebyshev, Elliptic 비교
Reference
로그인하면 댓글을 남길 수 있습니다.
[공지]회원 가입 방법
[공지]글 작성 및 수정 방법
음향/signal_processor/filter/filter_topology.txt · 마지막으로 수정됨: 저자 정승환