비트 심도
bit depth
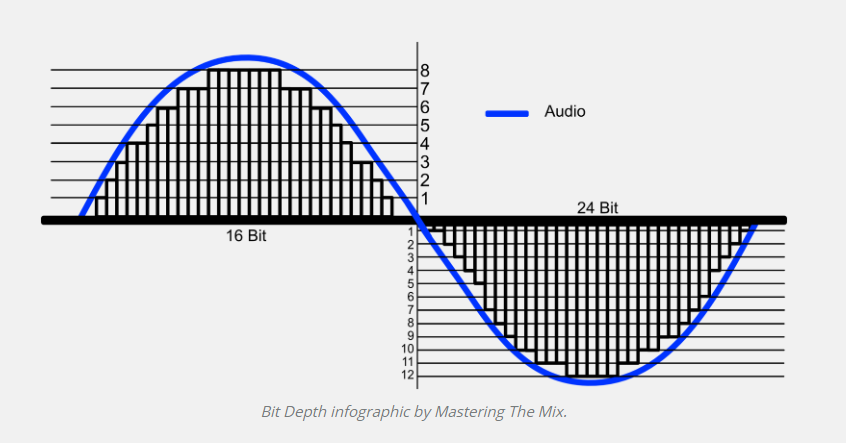
비트 심도는 디지털 오디오 시스템에서 샘플의 진폭을 얼마나 정밀하게 표현할 수 있는지를 결정하는 핵심 요소입니다. 이는 곧 다이내믹 레인지와 해상도에 직접적인 영향을 미치며, 오디오의 전체적인 품질과 밀접한 관련이 있습니다.
bit
A-D converting
4dBu 를 기준으로 헤드룸을 18dB 를 준 아날로그 입력을 디지털로 변환하는 A-D 컨버터 기준으로 예를 들면
| 아날로그 신호 | Vpp(peak) |
|---|---|
| 22dBu | 27.581673844 Vpp |
| 4dBu | 3.47232701Vpp |
| 0dBu | 2.19089023Vpp |
| -100dBu | 0.000021909 Vpp |
| -122dBu | 0.00000174 Vpp |
| -infinity | 0 Vpp |
즉 V (전압) 의 범위는 -122dBu ~ 22dBu 까지 0.00000174v~ 27.581673844v
즉 약 144dB의 범위에서
가장 큰 전압과 가장 작은 전압의 차이를 표현할 때 자리수의 범위는 “최소” 8자리가 필요하다.(소수점 -6자리 부터 소수점 위로 +2자리까지) 하지만, 자리수가 더 많아지면 더 자세한 표현이 가능하다. 24bit 가 144dB 표현이 가능하다는 말은 “최소” 라는 전제조건이 붙는 것이다.
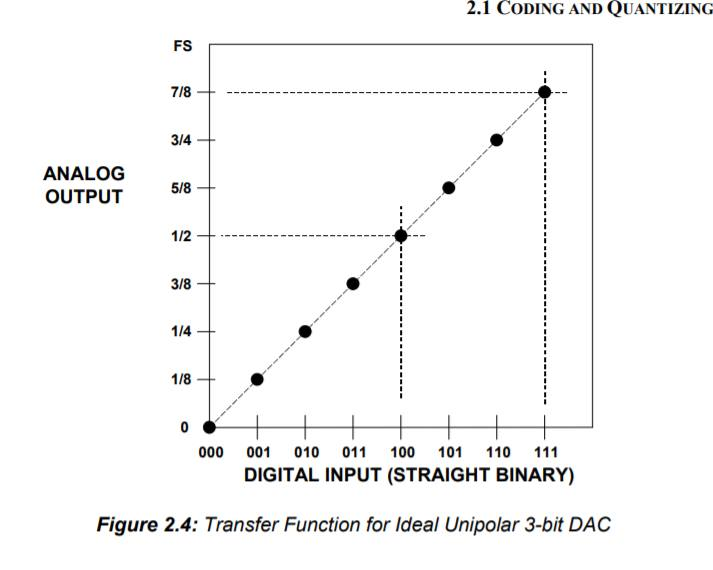
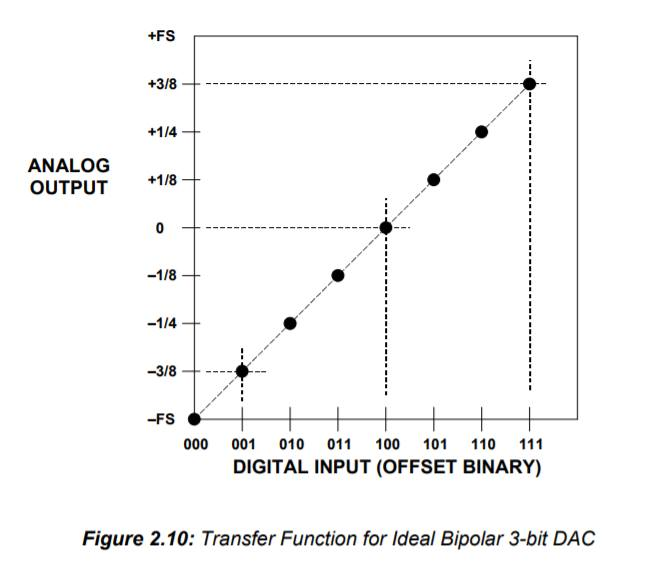
각 데이터 형식의 표현 범위
정수형 표현 범위
| 설명 | 계산식 | 결과 | 자릿수 |
|---|---|---|---|
| 최소 양수 정규화값 | 1.0 × 2-126 | 1.1754944 × 10-38 | 38자리 |
| 최대 양수값 | (2 - 2-23) × 2127 | 3.4028235 × 10+38 | 38자리 |
dBFS
dB full scale
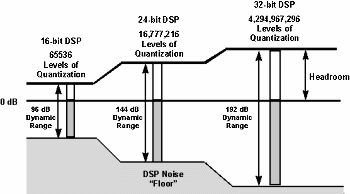
디지털 심도 포맷에 따라서 표현 가능한 최대값이 다 다르기 때문에(16bit:96dB, 24bit:144dB), 최대값이 통일이 안되어서 거꾸로 0을 최대값으로 - 단위로 표기한다. 또한 심도에 따라 표현 범위도 다 다르기 때문에 그 범위를 Full Scale 로 표현하게 된다. 일반적인 레퍼런스 레벨은 -18dBFS(24bit & above), -12dBFS(16bit)이다.
최대값의 진폭(Amplitude)의 절반값을 가지는 지점을 -6dBFS로 정해서, 값을 정한다. 다시 말해서 24bit(144dB) 던, 16bit(96dB)던, 48bit(288dB)이건 상관 없이 최대값을 0dBFS, 절반값을 -6dBFS로 정하기 때문에, 디지털 심도의 차이는 “해상도“의 차이로 나타난다.1)
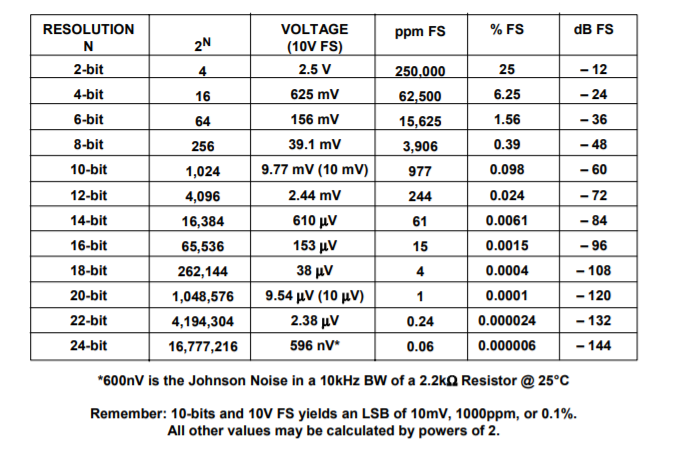
위의 표는 10V 를 각기 4bit, 16bit, 24bit 등으로 A-D 컨버팅 했을 때의 분해능, 해상도를 나타낸다.
https://en.wikipedia.org/wiki/DBFS
The level of 0 dBFS is assigned to the maximum possible digital level.[2] For example, a signal that reaches 50% of the maximum level has a level of −6 dBFS, which is 6 dB below full scale. Conventions differ for root mean square (RMS) measurements, but all Peak measurements smaller than the maximum are negative levels.
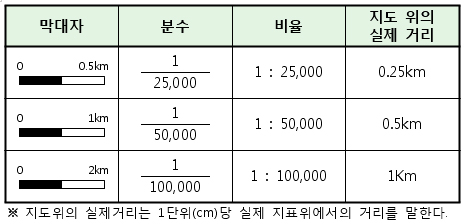
쉽게 요약하면 Full scale 은 지도에서 말하는 “축척” 과 같은 개념이다. 따라서 높은 심도는 파형을 더 세밀하고 자세하게 표현하게 된다. 2)
DSP 엔진
DAW
Cubase나 Logic 등의 DAW 에서 32bit 부동소수 포맷으로 프로젝트를 설정하고 사용하는 경우, 24bit로 녹음된 오디오는 추가로 8자리의 부동소수 표현을 위한 비트를 추가로 얻게 된다.
따라서, DAW 내부적으로 파형의 진폭이 0dBFS 이상으로 크게 변화하는 경우에도 클리핑 현상이 일어나지 않고 오디오 프로세싱이 가능하다.
24bit로 녹음된 데이터를 DAW에서 32bit 부동소수 포맷으로 사용할 시 레퍼런스 레벨인 -18dBFS를 기준으로 변환하기 때문에 해상도에 영향을 미치게 된다. 즉 예를 들면 24bit에서 32bit 부동소수로 변환 시 가장 큰 신호값인 0dBFS는 0dBFS로 일치하도록, -18dBFS는 그도 역시 32bit 부동소수 포맷의 -18dBFS로 full scale을 유지하게 된다. 그에 따라 시그널 처리의 해상도가 증가하게 된다. 기존 데이터의 값에는 변함이 없었지만 그 다음에 이 데이터를 가지고 DSP 처리를 하게 되면 더 세밀하고 정밀한 처리가 들어가게 되는 것이다.3)
특히, 이퀄라이저나 컴프레서와 같은 시그널 프로세서에서는 10dB, 20dB와 같은 높은 증폭 및 감쇄가 필요한 DSP 연산을 하게 된다. 20dB 정도이면 실제 디지털 숫자로는 큰 단위의 연산(100배 증폭 및 감쇄)이므로 심도가 상당히 중요하다고 볼 수 있다.
Fixed point dynamic range comparison
https://www.analog.com/-/media/analog/en/landing-pages/relationship-of-data-word-size/figure7.gif?la=en
정수 VS 부동소수
정수형 연산(Integer)과 부동소수형 연산(Floating point)을 비교하면, 정수형 연산의 장점은 부동소수형 연산보다 연산 클럭 수가 적게 들어가서 레이턴시 부분에서 유리하다.는 점이다. 하지만 최근에는 부동소수 DSP의 발전으로 인하여 큰 차이는 없다.
반면 부동소수점의 장점은, 매우 높은 해상도이다. 위에 항목들에서 설명했듯이 소수점을 유동적으로 변경할 수 있는 숫자 표시 양식 때문에, 부동소수점으로 표현할 수 있는 가장 큰 숫자는 정수형에서 표현할 수 있는 가장 큰 숫자보다 훨씬 큰 수를 표현하는 것이 가능하다.
레이턴시에 관한 문제 때문에, DSP 칩을 주력으로 사용하는 디지털 믹싱 콘솔이나, 디지털 시그널 프로세서들의 경우에는 40비트나 56비트 정수형 DSP를 사용하는 경우가 있지만 점점 32비트 부동소수형 DSP 또는 CPU 기반으로 바뀌는 추세이다.
Reference
[공지]회원 가입 방법
[공지]글 작성 및 수정 방법